УДК 510

 

Логачёва Людмила Фёдоровна,

преподаватель,

ФСПО Политехнический институт им. Н.Н. Поликарпова

ОГУ имени И.С. Тургенева,

Россия, Орёл

 

ИНТЕГРАЦИЯ ЗНАНИЙ ЭЛЕМЕНТАРНОЙ И ВЫСШЕЙ МАТЕМАТИКИ НА ПРИМЕРЕ ИЗУЧЕНИЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН

 

Аннотация: в данной статье демонстрируется колоссальная возможность применения знаний элементарной и высшей математики внутри самой математики. Статья показывает значимость, необходимость и неизбежность фундаментальных знаний математики на примере решения задач на непрерывные случайные величины в теории вероятностей и математической статистике.

Ключевые слова: математика, дифференциальная и интегральная функции распределения непрерывной случайной величины, формула, график, коэффициент, числовые характеристики.

 

 

Logacheva Lyudmila Fedorovna,

teacher,

FSVE Polytechnic Institute named after N.N. Polikarpova

OSU named after I.S. Turgenev,

Russia, Orel

 

INTEGRATION OF KNOWLEDGE OF ELEMENTARY AND HIGHER MATHEMATICS ON THE EXAMPLE OF STUDYING CONTINUOUS RANDOM VARIABLES

 

Abstract: this article demonstrates the enormous possibilities of applying the knowledge of elementary and higher mathematics within mathematics itself. The article shows the importance, necessity and inevitability of fundamental knowledge of mathematics by the example of solving problems on continuous random variables in probability theory and mathematical statistics.

Key words: mathematics, differential and integral distribution functions of a continuous random variable, formula, graph, coefficient, numerical characteristics.

 

Математика – язык исследований, основа любого образования. На современном этапе развития прикладных математических дисциплин призвана решать профессиональные задачи во всех сферах деятельности человека. В этой связи усиливается её роль, как фундаментальной науки.

Цель обучения математике на факультете СПО состоит в том, чтобы студент, во-первых, получил фундаментальную математическую подготовку в соответствии с программой, а во-вторых, овладел навыками математического моделирования в области будущей профессиональной деятельности.

Фундаментальная математическая подготовка выпускника является основой для его будущей профессиональной жизни. Так как именно фундаментальные знания обеспечивают выпускнику возможность понимать и осваивать современную технику, новейшие технологии и новые принципы организации производства. Многие наши выпускники, состоявшиеся профессионалы своего дела, благодарны своим преподавателям за полученные знания: как для профессионального роста, так и для самореализации, уверенности и удовлетворённости своих амбиций.

Говоря о приложениях математики, нам кажется, во-первых, что она применяется в смежных дисциплинах. Например, в физике, астрономии, информатике. Во-вторых, без математики не обходятся технические и специальные дисциплины. То есть математика является таким аппаратом, который служит другим наукам, математика – это «производная» для изучения всего того, что вокруг нас развивается. Даже там, где, казалось бы, не нужна математика, например, в философии, педагогике и психологии, без неё всё же не обойтись.

Но нельзя забывать о применении математики внутри самой математики. Так изучив тригонометрию, мы используем её для изучения комплексных чисел, в интегральном исчислении – для применения универсальных подстановок, в функциональных рядах – для суммирования бесконечного числа слагаемых, которое в свою очередь применяется в компьютерных технологиях, в частности, в программах микрокалькуляторов и т.д. Наибольшее количество математических знаний интегрируются при изучении теории вероятностей и математической статистики.

Изучив элементарную теорию вероятности, и, переходя к изучению непрерывных случайных величин, мы сталкиваемся с вычислением несобственных интегралов. И хотя, исследуя непрерывные случайные величины, можно обойтись несобственными интегралами первого рода, т.е. от неразрывных функций, решение таких интегралов требует серьёзной подготовки в области математического анализа. К тому же, важными навыками при решении задач по теории вероятностей и математической статистике являются приобретённые из элементарной математики умения строить и читать графики, устанавливать соответствие между величинами, умения пользоваться формулами и таблицами.

Приведем примеры задач по теории вероятностей и математической статистике, при решении которых используется огромное количество математических знаний, умений и навыков из элементарной и высшей математики.

Решить задачи, используя общие методы определения числовых характеристик непрерывной случайной величины, полученные результаты сравнить со значениями, вычисленными по специальным формулам для числовых характеристик показательно распределённой НСВ. Сделать выводы.

Задача. Непрерывная случайная величина (НСВ) Х задана интегральной функцией распределения: .

Требуется:

1) определить коэффициент А;

2) найти дифференциальную функцию (плотность) распределения вероятностей ;

3) схематично построить графики интегральной  и дифференциальной  функций распределения НСВ;

4) вычислить математическое ожидание и дисперсию НСВ Х;

5) определить вероятность того, что случайная величина Х примет значение из интервала .

Решение:

1)  В силу непрерывности функции распределения: . Значит, .

2)  Найдём функцию плотности распределения:

. Значит, .

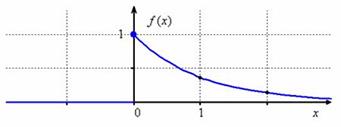
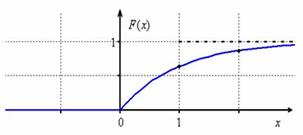
3)  Графики функций распределения и  имеют вид:

4)  Вычислим математическое ожидание и дисперсию НСВ Х. Есть короткий путь (по готовым формулам), и есть универсальный. Начнём с универсального: общая формула математического ожидания приводит нас к следующему несобственному интегралу:.

Сначала найдём неопределённый интеграл:  по частям (т.е. по формуле:). Постоянную интегрирования опустим для краткости.

. Итак, .

Дробь  т.к. знаменатель имеет более высокий порядок роста, чем числитель.

Дисперсию вычислим по формуле: . Для этого отдельно вычислим несобственный интеграл .

Как и в случае с математическим ожиданием, сначала найдём интеграл: .

Нужно дважды интегрировать по частям. Решение упрощается тем, что после первого применения формулы  мы получаем  только что решённый интеграл (постоянную интегрирования опустим для краткости):

Таким образом, несобственный интеграл:

.

Здесь дробь   по той же причине – порядок роста.

И, наконец, дисперсия: .

5) .

Далее студентам предлагается удостовериться в правильности найденных числовых характеристик общими методами: полученные результаты сравнить со значениями, вычисленными по специальным формулам для числовых характеристик и сделать выводы.

Задача 2. Непрерывная случайная величина Х задана своей плотностью распределения:.

Требуется:

1) определить коэффициент А;

2) найти интегральную функцию распределения вероятностей ;

3) схематично построить графики интегральной  и дифференциальной  функций распределения НСВ.

Решение:

1)  В силу условия нормировки: несобственный интеграл от плотности вероятности НСВ в бесконечных пределах равен единице, т.е. .

В данной задаче  состоит из двух частей, поэтому:.

Получили уравнение относительно параметра А: .

Правый интеграл равен нулю, а левый: .

Таким образом, наше уравнение превратилось в результат:  и функция плотности: .

2) Функцию распределения НСВ отыскиваем через её плотность вероятности: , собирая  на двух промежутках:

1. На промежутке ,  следовательно:

– получилась экспонента.

2. На интервале :  и:

, что и должно получиться по свойству интегральной функции НСВ.

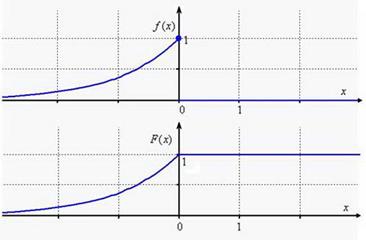
3. Для построения графиков используем опорные точки: ,  и прочерчиваем части экспонент с соответствующими дополнениями:

Итак, для демонстрации колоссальных возможностей применения знаний элементарной и высшей математики внутри самой математики рассмотрены два примера задач на показательно распределённую случайную величину, заданную интегральной или дифференциальной функцией распределения. Эти задачи, а также задачи на другие виды распределения, например, равномерное или нормальное, решают как общими методами, т.е. используя свойства функций распределения  или  и формулы нахождения числовых характеристик, так и частными методами, т.е. по конкретным формулам для вычисления числовых характеристик НСВ Х, распределенных по соответствующим законам.

Для решения таких задач интегрируются знания из различных разделов элементарной и высшей математики: понятие функции, способы её задания, чтение и построение графиков функций (в том числе с помощью Excel); дифференциальное и интегральное исчисления, знание формул и умение вычислять по формулам с помощью инженерного микрокалькулятора или функции Excel. При этом, сравнивая полученные результаты, студенты имеют возможность убедиться в непротиворечивости решения задачи и безусловной научности математики.

Решение задач на НСВ в теории вероятностей и математической статистике демонстрирует необходимость, неизбежность и значимость математических знаний элементарной и  высшей математики.

 

 

Список литературы:

 

1.   Кремер Н.Ш. Теория вероятностей и математическая статистика. М.: ЮНИТИ, 2010.